Leonardo de Pisa y las revelaciones matemáticas del “Liber abaci”

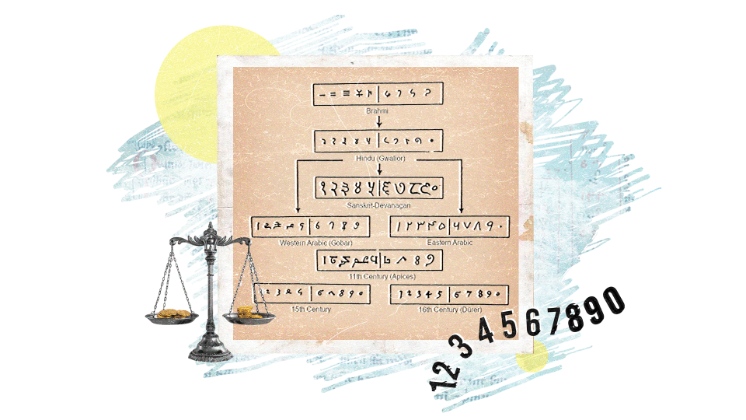
Las nueve cifras hindúes son: 9 8 7 6 5 4 3 2 1. Con estas nueve cifras y con el símbolo 0, que los árabes llaman cefir, cualquier número puede ser escrito, como se demuestra a continuación. (Fibonacci, trad. 2002)

Así comienza Leonardo de Pisa a redactar el primer capítulo de su obra Liber abaci, o Libro del cálculo, publicada por primera vez en el año 1202. En este libro, el autor presenta de manera magistral el sistema de numeración decimal, la notación posicional y los métodos de cálculo para resolver sumas, restas, multiplicaciones y divisiones. Además, dedica extensas páginas a problemas matemáticos vinculados con el comercio: pesos, medidas, monedas e interés; también, proporcionalidad, ecuaciones, raíces cuadradas y otros tantos resultados intramatemáticos relacionados con la aritmética, el álgebra y la geometría.

Liber abaci es una obra maestra de Leonardo. Un legado cultural que influyó tanto en su época como en el desarrollo posterior de la matemática como ciencia. Por ello, Liber abaci es un clásico de la matemática.

No se trata de un libro que actualmente sea fuente de consulta de un matemático ni forma parte de la bibliografía de una currícula en la disciplina. Su estilo de redacción, con un lenguaje desprovisto de gráficos y fórmulas, no se corresponde con la estructura actual de los textos de matemática que abundan en teoremas y rigurosas demostraciones. Pero no por ello la matemática de Liber abaci es obsoleta, por el contrario, sigue vigente, por lo que vale la pena sumergirse en su lectura, sentir cómo Leonardo –con su mayor dedicación y de manera gradual– nos enseña desde la escritura de los primeros números hasta la resolución de complejas ecuaciones algebraicas.

Para comprender el contexto en que este libro fue escrito, nos situamos en la época en que vivió su autor. Leonardo de Pisa (1170-1240, aproximadamente), también conocido como Leonardo Pisano, fue un ciudadano de la República de Pisa, en la actual Italia. Su padre, Guglielmo Bonacci, era un comerciante que trabajaba en Bugía, Argelia, al norte de África. Por ello, actualmente a Leonardo da Pisa se lo conoce también como Fibonacci (filius [hijo] + Bonacci), aunque no es el nombre con el que se lo conocía en su época.

Hacia finales del siglo XII y comienzos del siglo XIII, luego de una confusa época posterior a la caída del Imperio romano, comenzó en Europa a resurgir la economía, la cultura y el conocimiento. El intercambio comercial entre ciudades ubicadas sobre el mar Mediterráneo estaba en su auge. Pisa y otras ciudades marítimas –como Génova y Venecia– eran de fundamental importancia para el comercio mediterráneo.

Leonardo acompañaba a su padre. Fue él quien lo impulsó a estudiar matemática en Bugía durante su juventud. Allí tuvo, según él mismo cuenta, “una maravillosa instrucción en el arte de las nueve cifras hindúes” (Fibonacci, trad. 2002), y su educación en la matemática continuó con maestros en distintos lugares como Egipto, Siria, Grecia, Sicilia y Provenza. Leonardo se formó y fue un brillante matemático en su época, imbuido de las distintas culturas europeas, hindúes y árabes; conocedor, por lo tanto, del álgebra de Al-Jwarizmï, de los Elementos de Euclides, del legado de Pitágoras. Pero también Leonardo conoció el oficio del comercio y los problemas matemáticos que implicaban el intercambio de mercaderías, la equivalencia entre monedas, el uso de distintas medidas de peso, el cálculo del interés, entre otros. La complejidad de los problemas requería utilizar métodos eficientes de cálculo para quien quisiera ser exitoso en los negocios. Saber hacer cuentas y resolver problemas matemáticos era imprescindible.

En aquel entonces, las ciudades europeas continuaban con el uso del sistema de numeración romano con los símbolos que actualmente conocemos: I, V, X, L, C, D y M. Con ellos se escribían los números y también se hacían cálculos. Resolver cuentas en este sistema no era tarea sencilla ni lo es hoy: invitamos al lector a calcular algunas operaciones en números romanos (sin traducir al sistema decimal) como sumar XIV con LVIII, restarle VII a XXI, multiplicar XXX por V o dividir MMCII por XVIII.

¿Cuál sería un buen algoritmo para realizar estas cuentas en números romanos? En la Edad Media existían diferentes técnicas y reglas de cálculo, se usaban tablas y ábacos, todo lo cual requería de cierto conocimiento específico. Los comerciantes debían entender estas herramientas, de lo contrario se veían en la obligación de contratar a expertos, llamados calculistas, que pudieran asistirlos en la tarea.

Leonardo de Pisa, entre tanto, había aprendido el uso del sistema indoarábigo para la numeración, además de los algoritmos para resolver las operaciones básicas en este sistema, que era mucho más avanzado y eficiente que el de numeración romano. Se hacía imperativo introducir este cambio, que favorecería el desarrollo y auge del comercio europeo –y, por supuesto, también el del conocimiento científico–.

Así fue que Leonardo de Pisa escribió Liber abaci, el libro del cálculo.

Liber abaci

La obra está compuesta por quince capítulos. Referirnos a cada uno de ellos escapa al objetivo de este artículo. Nos enfocaremos en los primeros, que tienen un abordaje accesible y cuya lectura no nos aporta mayor conocimiento matemático; sin embargo, merece la pena reflexionar sobre la forma en que Leonardo introduce los conceptos básicos de la aritmética.

Leonardo se dirigía a un público que conocía y utilizaba la matemática. Su objetivo era brindar una nueva herramienta, para él más eficiente, y enseñar cómo usarla. Pero también, inconsciente o deliberadamente, mantuvo algunas prácticas de cálculo que ya se utilizaban, como aquel docente que apela al conocimiento previo de sus estudiantes para abordar nuevos aprendizajes. Un verdadero maestro.

El lector para el que escribe Leonardo tiene conocimiento de los números, sabe contar y puede hacer operaciones matemáticas. Lo que presenta de novedad en los primeros capítulos es la escritura o representación escrita de estos números y los algoritmos de cálculo. Así, empieza por explicar detalladamente el uso de las cifras del 1 al 9 para representar distintos números y enfatiza que cualquier número, por grande que sea, siempre podrá ser escrito. Para ello, refuerza el uso de la notación posicional: la primera cifra es para las unidades, la segunda (a su izquierda) para las decenas –o dieces–, la tercera para las centenas –o cientos–, y así sucesivamente.

2

32

432

dos

treinta y dos

cuatrocientos treinta y dos

También introduce el uso del símbolo 0 para representar que no se colocan cifras significativas en esa posición: para escribir dos centenas y nueve unidades, se anota 209, donde el 0 indica que no hay decenas y reserva el lugar en esa posición.

9

209

nueve

doscientos nueve

Es de notar que el sistema de numeración romano también hace uso de una base decimal: los símbolos X (diez), L (cincuenta), C (cien), D (quinientos), M (mil) corresponden a un múltiplo o a una potencia de diez. Es un sistema aditivo en tanto que el número representado se asocia con la adición o la resta de los valores representados por los símbolos según su posición relativa: XXVII es XX (veinte) más V (cinco) más II (dos), es decir, veintisiete. IV es V (cinco) menos I (uno), que es cuatro. Es por ello que los nombres con los que Leonardo designa los números, y que son los mismos que se aplicaban a la antigua numeración romana, son coherentes (salvo excepciones) con la escritura decimal y notación posicional. Por ejemplo, XXXII y 32 se nombran ambos triginta duo en latín, haciendo referencia a tres veces diez y un dos, o treinta y dos en español.

Ahora bien, Leonardo explica que este nuevo sistema de numeración también permite representar números muy grandes, y para ello se deben emplear una buena cantidad de cifras.

¿Cómo se nombrarían ahora los números con seis, siete, ocho o más cifras? En primer lugar, las cifras del número se agruparían de a tres, comenzando de derecha a izquierda y, a partir del segundo grupo, se haría referencia a los miles, los miles de miles, los miles de miles de miles, y así. Escribir y nombrar grandes números ya no sería imposible:

27 892: veintisiete mil ochocientos noventa y dos.
4 567 892: cuatro mil mil, quinientos sesenta y siete mil ochocientos noventa y dos.

1 234 567 892: un mil mil mil, doscientos treinta y cuatro mil mil, quinientos sesenta y siete mil ochocientos noventa y dos.

Claro está que hoy en día utilizamos el término de millón, mil millones, billones, pero aquella fue la solución primera de Leonardo. Luego, el pisano se introduce en cómo resolver las operaciones matemáticas elementales –suma, resta, multiplicación y división–, explicitando tablas y algoritmos para hacer los cálculos de manera eficiente. Por ejemplo, la tabla de la suma para el 2 incluye:

2 + 2 = 4
2 + 3 = 5
2 + 4 = 6

Y así sigue. La tabla de la suma para el 3 comienza en 3 + 3 = 6, obviando 3 + 2 = 5 pues 2 + 3 ya estaba en la tabla del 2. Se daba por entendido que la suma es conmutativa.

En su explicación sobre el uso de los algoritmos, Leonardo señala que será necesario tener una pizarra para escribir y una mano para “guardar números”. Con “guardar números” Leonardo se refería al acarreo. Así es: usar los dedos para representar números era una práctica habitual, pero no en la forma que lo hacemos actualmente. Hoy usamos los cinco dedos de la mano para representar el 5, pero no es así como aparece en Liber abaci. El método utilizado servía para contar o representar cualquier número desde el uno hasta el noventa y nueve usando los dedos de una sola mano. El pulgar y el índice, con distintas disposiciones, se usaban para indicar la decena, mientras que los otros tres dedos para los números del uno al nueve. Leonardo incluye en su libro la explicación y un dibujo de este tipo de conteo.

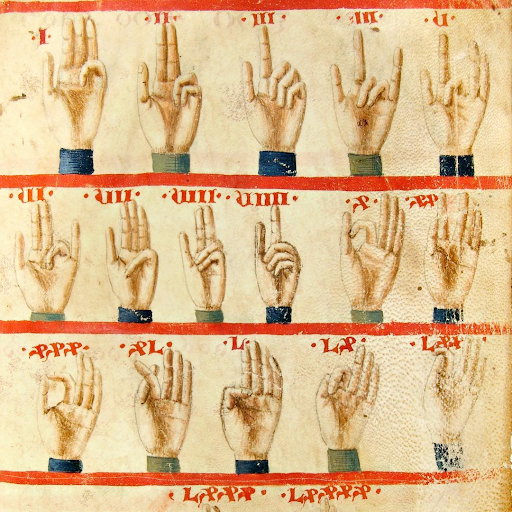
Las páginas de Liber abaci contienen múltiples ejemplos de cálculos explicados paso por paso, y varios de ellos se ilustran en el margen de la hoja. Si bien los algoritmos que explica Leonardo no difieren en gran medida de los que hoy en día usamos, se acudía más al cálculo mental –en este caso, cálculo mental refiere a resolver mentalmente algunas cuentas sencillas antes de plasmarlas en el papel–. Por eso, primero enseñó las tablas.

Invitamos al lector a tomar lápiz y papel y seguir el siguiente ejemplo de una multiplicación tal cual la explicaría Leonardo en Liber abaci. Recordemos que en aquel entonces no se utilizaban símbolos especiales como +, -, × o ÷ para indicar las operaciones, sino que el desarrollo era en un lenguaje más coloquial.

Si se quisiera multiplicar 56 por 32 deben seguirse los siguientes pasos:

En primer lugar, deben encolumnarse los números según las posiciones de sus cifras (unidades con unidades, decenas con decenas), y en la parte superior se irá anotando el resultado.

resultado
56
32

Se debe comenzar multiplicando las unidades de ambos números (la primera cifra de la derecha), y el valor obtenido contribuirá a las unidades del resultado. En este caso, se multiplica 2 con 6, que tiene por resultado 12. Se anota el 2 y el “1 se guarda en la mano”.

2

56

32

Luego se multiplican la decena de 56 (el 5) por la unidad de 32 (el 2) y la unidad de 56 (el 6) por la decena de 32 (el 3). Es decir, 5 por 2 más 6 por 3, que resulta igual a 28. Porque, dice Leonardo, decenas por unidades da lugar a decenas. Al 28 se le suma el 1 que está en la mano. El resultado es 29. Se anota el 9 en las decenas del resultado y “se guardan 2 en la mano”.

92

56

32

Por último, se multiplica el 5 con el 3 –porque, siguiendo el razonamiento de Leonardo, decenas con decenas da centenas–, se agregan los 2 de la mano y el resultado es 17. Como ya no quedan cálculos que hacer, se anota el 17 en el resultado:

1792
56
32

¿Puede reconocer el lector las semejanzas y diferencias con el algoritmo convencional que hoy se utiliza? ¿Qué pasos se agregarían al cálculo si la cuenta fuese 156 por 32? Leonardo de Pisa no explica el porqué de los algoritmos ni de su correcto funcionamiento. Los presentó como lo que eran –y siguen siendo hasta el día de hoy–: una herramienta de cálculo eficiente, superior al ábaco y a otras tablas que se usaban en la época. Se requería de un poco de memoria para recordar las operaciones con números pequeños, y también de los dedos, que serían útiles para el acarreo. La habilidad en el uso de los algoritmos sería necesaria más adelante, para resolver otros problemas matemáticos.

Como mencionamos anteriormente, con el sistema decimal Leonardo de Pisa incursiona tanto en las operaciones matemáticas básicas como en problemas matemáticos vinculados a proporcionalidad, resolución de ecuaciones, raíces, álgebra y geometría.

Por último, debemos aclarar que Leonardo no fue el único ni el primero en intentar introducir en Europa la numeración indoarábiga. Hubo otros, como Gerberto de Aurillac (945-1003, aproximadamente), que hicieron importantes aportes varios siglos antes.
Pero, sin duda, la obra Liber abaci de Leonardo de Pisa fue la que mejor sirvió a la difusión de nuestro actual sistema de numeración.

Descargar PDF